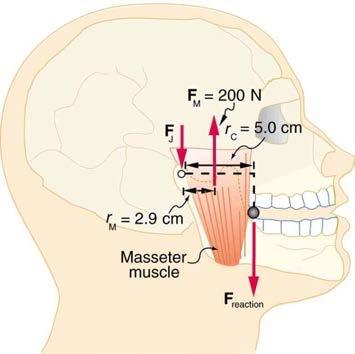
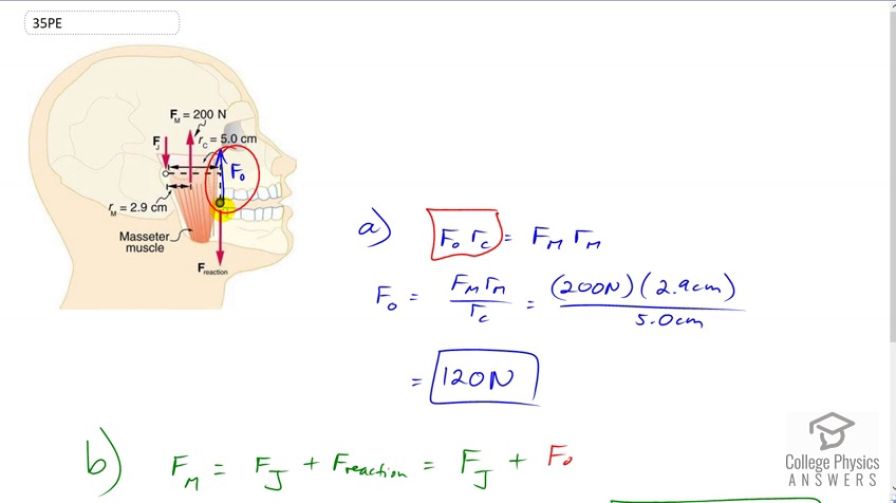
a)
b)
Solution video
OpenStax College Physics, Chapter 9, Problem 35 (Problems & Exercises)
Calculator Screenshots
Comments
Where did the 120N come from? (200*2.9)/5 = 116.
In the old days, people would "bite the bullet" to prevent screaming when something painful was going to happen (like a leg amputation). Funny they should include this in physics problems!
Shouldn't 2.9 cm and 5.0 cm be converted to meters before the calculation?
That's a great question zach. It's normally a really good routine to convert to "m.k.s" units (meters, kilograms, seconds) as you're suggesting. I can get away with a shortcut in this particular solution, leaving the measurements in centimeters, since the lengths will be divided. When divided, the units will cancel. It's important that the length units are the same, but they can be any length unit, just so long as they're the same length unit.
All the best,
Shaun




