Question
The Sun radiates energy at the rate of from its surface into dark empty space (a negligible fraction radiates onto Earth and the other planets). The effective temperature of deep space is . (a) What is the increase in entropy in one day due to this heat transfer? (b) How much work is made unavailable?
Final Answer
Solution video
OpenStax College Physics, Chapter 15, Problem 51 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
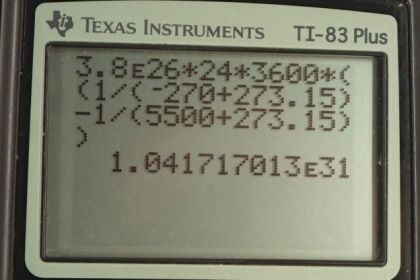
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The sun radiates 3.8 times ten to the 26 watts of power from its surface and its surface temperature is 5500 degrees Celsius and it's readily eating this energy into deep space which has a temperature of minus 270 degrees Celsius. So we're asked to find the total change in entropy during a full day and that's going to be the change in entropy of the surface of the sun plus the change in entropy of deep space. Now change in entropy is the amount of heat transferred into system divided by its temperature. And so we can replace each of these terms here with Q over T. So in the case of the Sun surface we have a negative Q because the heat is leaving the surface and so the amount transferred into the surface is negative and we divide by the absolute temperature of the surface of the sun and then add to that the heat transferred into deep space divided by deep space’s absolute temperature and so we can factor out Q and then switch the things around to have a minus on the right. So we have Q times one over deep space temperature minus one over Sun's surface temperature. Now to find Q, we need to use this power formula which is the amount of energy released per time and we’ll multiply both sides by t and then switching sides around and we have Q equals power times time. So the total change in entropy, then, is Pt times one over TDS minus one over Ts. So it’s 3.8 times tenth to the 26 watts of power multiplied by the time which is one day we have to convert that into seconds though. So, we multiply a day by 24 hours per day and then times by 3600 seconds per hour then times by one over minus 270 degrees Celsius plus 273.15 to convert this into Kelvin. This is the temperature of deep space and then minus one over the absolute temperature of a surface which is 5500 degrees Celsius plus 273.15. This works out to 1.04 times tenth to the 31 joules per Kelvin is the change in entropy of the sun deep space system in a day. Now the amount of work that has become unavailable is the changed entropy times by the lowest temperature that we're dealing with. So this is 1.0417 times tenth to the 31 joules per Kelvin change in entropy that we’ve found in part a multiplied by the temperature of deep space in absolute terms. This works out to 3.28 times ten to the 31 joules.