Question
An RLC series circuit has a resistor and a 25.0 mH inductor. At 8000 Hz, the phase angle is . (a) What is the impedance? (b) Find the circuit’s capacitance. (c) If is applied, what is the average power supplied?
Final Answer
Solution video
OpenStax College Physics, Chapter 23, Problem 105 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
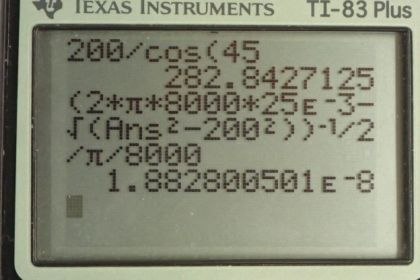
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have an R L C circuit where the phase angle is 45 degrees, the resistance is 200 ohms, and the inductance is 25 millihenries, and the frequency is 8000 hertz. Part A asks us to find the impedance. Now, we know the phase angle, so we can use this formula for the power factor which is cosine of that phase angle equals R over impedance to calculate impedance. So, we're going to solve for Z by dividing both sides by cos phi and multiply both sides by Z. So, impedance is resistance divided by cosine of the phase angle. So, that's 200 ohms divided by cos 45 which is 283 ohms. In Part B, we're going to use this value that we found for impedance and the known values for inductance and resistance to figure out what is the capacitance. So, impedance is square root of R squared plus the difference between the inductive reactants minus the capacitive reactants squared. So, we're going to solve this for the capacitive reactants and then we'll substitute the capacitance in for that Xc and then solve for that. So, let's square both sides to begin with. And so, we have impedance squared equals resistance squared plus Xl minus Xc squared. And then, we'll isolate this factor by subtracting R squared from both sides and then switch the sides around. And then we have Xl minus Xc squared equals Z squared minus R squared. And then we'll take the square root of both sides to get Xl minus Xc equals square root of Z squared minus R squared. And then, let's add Xc to both sides and then also subtract this square root, so that's square root minus R squared from both sides. And, this makes Xc equals Xl minus square root Z squared minus R squared. Now, at this point we need to substitute for each of this reactant's formulas. So, for the inductive reactants, we'll substitute two pi F L. And then, for the capacitive reactants, we'll substitute one over two pi F C, and so I've done those substitutions in red here. Now, we're trying to solve for C and it's in the denominator here, so let's get it in the numerator by taking the reciprocal, by raising this side of the equation to the power negative one. And, what we do to one side we must also do to the other, and so we raise the other side to the power of negative one. This makes two pi F C equal two pi F L minus Z squared minus R squared all to the negative one. It looks strange, but it's true. And then, we'll divide both sides two pi F to finally solve for capacitance. So, capacitance equals two pi F times inductance minus square root of impedance squared minus resistance squared all to the negative one, then divided by two pi intense frequency. So, that's two pi times 8000 hertz times 25 millihenries minus square root of the impedance that we found at Part A, 282.843 ohms squared minus the resistance of 200 ohms squared. Square root that difference and then take this whole result to the power of negative one, then divide by two times pi times 8000 hertz, giving us a capacitance of 18.8 nanofarad. Now, the average power dissipated by the circuit is the RMS voltage times the RMS current times cosine of the phase angle, or this is the power factor in other words. And, we can find the RMS current by taking the RMS voltage divided by the impedance because we know both of those thing. And so, we'll substitute that in place of I. And so, the average power dissipated then is going to be voltage squared divided by impedance times cosine of the phase angle. So, that's 408 volts squared divided by the impedance of 282.843 ohms times cosine of 45 degrees, which gives a power dissipated of 416 watts.