Question
People with good hearing can perceive sounds as low in level as at a frequency of 3000 Hz. What is the intensity of this sound in watts per meter squared?
Final Answer
Solution video
OpenStax College Physics, Chapter 17, Problem 21 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
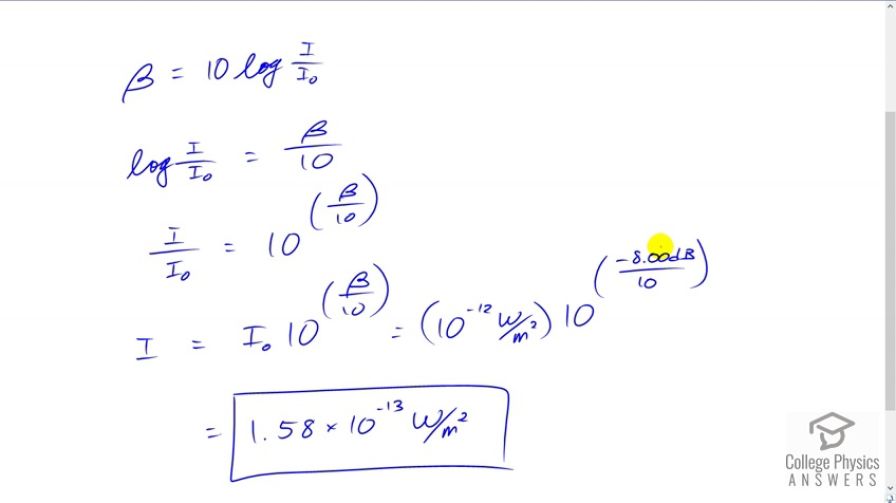
This is College Physics Answers with Shaun Dychko. We are going to find the intensity of a sound that has a sound intensity level of negative eight decibels. So, the formula for sound intensity level Beta is ten times logarithm of the intensity in watt per square meter divided by the reference intensity I naught which is the threshold of hearing. So, we going to divide both sides by ten because our job is to solve for I and given the beta of negative eight decibels and then we switch the sides around to get the unknown on the left and then we will make both sides power of ten and then left side that will make into I over I naught and on the right side its ten to the power of beta over ten. Then multiply both sides by reference intensity I naught and we are left with intensity I. So, I is I naught times ten to the power of decibel divided by ten. So, ten to the minus twelve watt per square metre times ten to the power negative eight decibels over ten which is 1.58 times ten to the minus 13 watt per square metre.
