Question
If your body has a density of , what fraction of you will be submerged when floating gently in: (a) Freshwater? (b) Salt water, which has a density of ?
Final Answer
- 99.5% submerged
- 96.9% submerged
Solution video
OpenStax College Physics, Chapter 11, Problem 39 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
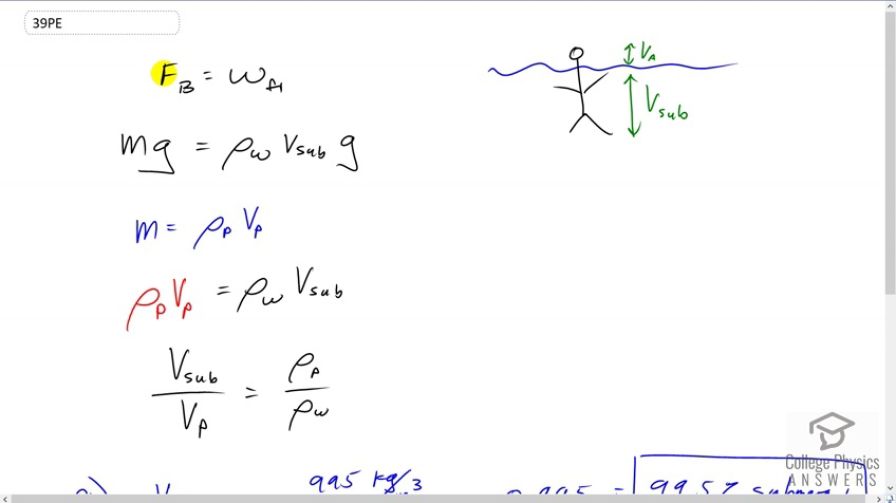
This is College Physics Answers with Shaun Dychko. The buoyant force on your body equals the weight of the fluid that your body displaces, that is Archimedes' principle. And the volume of fluid displaced is going to be the volume of your body submerged and there’s going to be some volume of your body above the water too here. Now this buoyant force also has to equal the total weight of the person in order for them to be floating and so I’ve written mg in place of F B here. Now we’re going to substitute the mass of water displaced because density is mass over volume and so you can solve for m by saying it’s density multiplied by volume and the volume of water is going to be equal to the volume of the person submerged, and then we multiply this by g to get the weight of the water displaced. And so that’s the buoyant force and mg also is the buoyant force because the person is floating and so the buoyant force is balancing the weight. And we can substitute for the total mass in terms of the person’s volume as well by going density of the person times total volume, so we have rho sub p for person times the person’s volume equals the density of water times the volume submerged. And now we can get a fraction submerged by dividing Vsub by Vp and then we’ll isolate that fraction by also dividing by the density of water. So we have the fraction submerged is the density of the person divided by the density of water. So that is 995 kilograms per cubic meter density of the person that we’re given, divided by the density of fresh water which is one times ten to the three kilograms per cubic meter, and this works out to 99.5 percent submerged. If the same person with the same density was floating in salt water, salt water has a slightly higher density of 1027 kilograms per cubic meter, this works out to 96.9 percent submerged.


