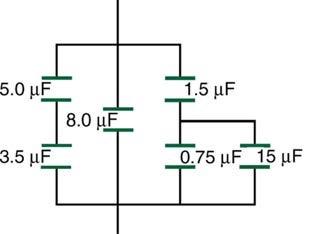
Question
Find the total capacitance of the combination of capacitors shown in Figure 19.34.
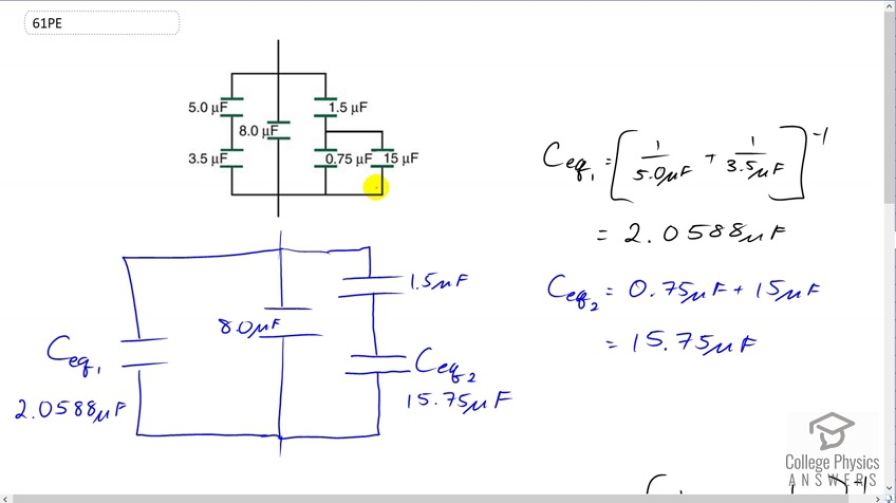
Final Answer
Solution video
OpenStax College Physics, Chapter 19, Problem 61 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
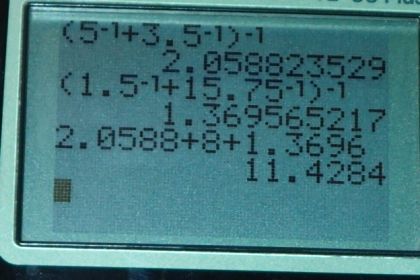
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to find the equivalent capacitance of this entire circuit, and it's important to take it step by step so it doesn't seem overwhelming. Now, we're going to rewrite the circuit as shown in this diagram here, where I've copied the 1.5 microfarads unchanged. I copied the eight microfarads unchanged. But the differences are that I combined these two capacitances into capacitance equivalent one, and then combined these two capacitances into capacitance equivalent two. And so, the next step would be to combine these two. And then, the third step will be to combine all three in parallel. Okay. So, the equivalent capacitance one is going to be the result of these two combined together. And, since they are in series, we take the reciprocal of each one, add them together, and then take the reciprocal of that sum. And so, this works out to one over five plus one over 3.5, giving us 2.0588 microfarads, keeping lots of decimal places because this is an intermediate in calculation. And then, in the equivalent capacitance two, because these are in parallel, we can take the direct arithmetic sum of the two capacitances to get their equivalent. So, 0.75 plus 15 microfarads gives 15.75 microfarads, and that's what's written here. Then, we're going to rewrite this schematic as this one. And, I copied Ceq1 unchanged, I copied eight microfarads unchanged, and then this one and a half microfarads plus Ceq2 will be replaced with C equivalent three. And so, because these are in series, we take the reciprocal of the first, one over one-half, plus the reciprocal of the second, one over 15.75, and then take the sum of those two, and then the reciprocal of that sum, giving us 1.3696 microfarads. Then, the equivalent capacitance of all three of these is going to be the final answer, or the total equivalent capacitance. That's going to be Ceq1 plus eight microfarads plus Ceq3. We're going to just take the arithmetic sum of them because they are in parallel. So, we have 2.0588 microfarads plus eight microfarads plus 1.3696 microfarads, giving us 11.4 microfarads is the total capacitance of the entire circuit.