OpenStax College Physics, Chapter 26, Problem 21 (Problems & Exercises)

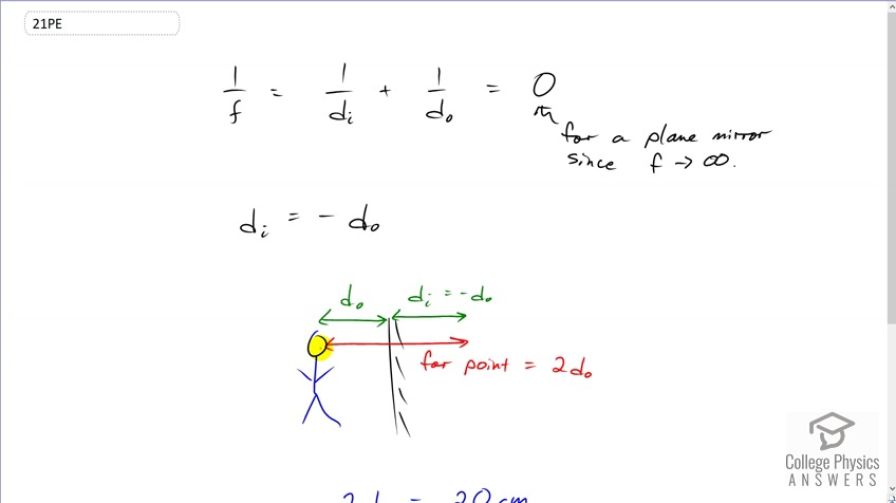
This is College Physics Answers with Shaun Dychko. So this man has a far point of 20 centimeters and the question is, how far should he stand from the mirror in order to see his beard when he's shaving it. So, first we need to figure out where is the image going to be when he's looking in the mirror. And, we'll figure out that the image distance is equal in magnitude to the object distance, which is on the other side of the mirror. So, one over the focal length of the mirror is reciprocal of the image distance plus reciprocal of the object distance but the focal length is infinity because it's a plain mirror and it doesn't have a focal length. It's going to reflect parallel rays parallel. So, parallel lays that come in to the mirror are going to be reflected back parallel and it will never converge. And so, for that reason, you can say that the focal point is basically at infinity. So, that makes this zero. One divided by a really big number is zero. And then, when you subtract one over object distance from both sides and you take the reciprocal of both sides, you find that the image distance is equal to the object distance but on the other side of the mirror. That's what that negative sign means. So, the image will be here. And, since the person's far point is 20 centimeters, this whole distance between their eye and where the image is has to be 20 centimeters and that distance is going to be two times the object distance because because we just discovered that the image distance is equal in magnitude to the object distance. So, their far point is two times the object distance or the distance from the mirror. And, two times that is 20 centimeters, and so we divide both sides by two to find that the distance they have to stand from the mirror is 20 divided by two, which is ten centimeters.