Question
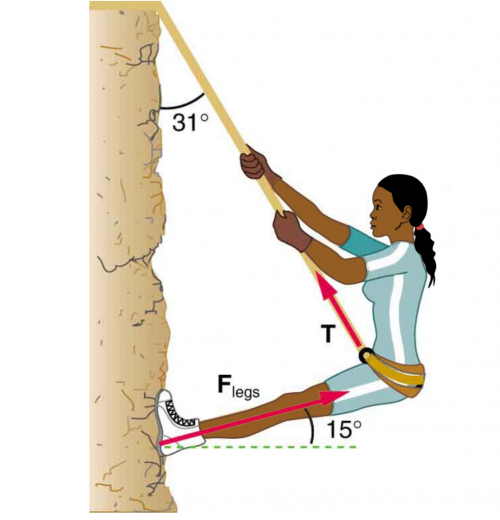
Consider the 52.0-kg mountain climber in Figure 5.20. (a) Find the tension in the rope and the force that the mountain climber must exert with her feet on the vertical rock face to remain stationary. Assume that the force is exerted parallel to her legs. Also, assume negligible force exerted by her arms. (b) What is the minimum coefficient of friction between her shoes and the cliff?
Final Answer
a)
b)
Solution video
OpenStax College Physics, Chapter 5, Problem 17 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
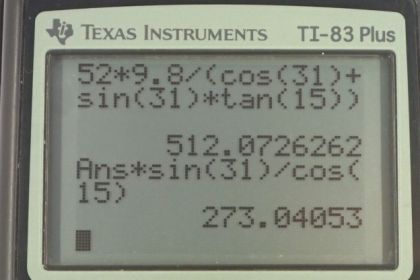
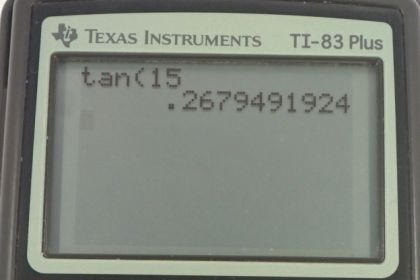
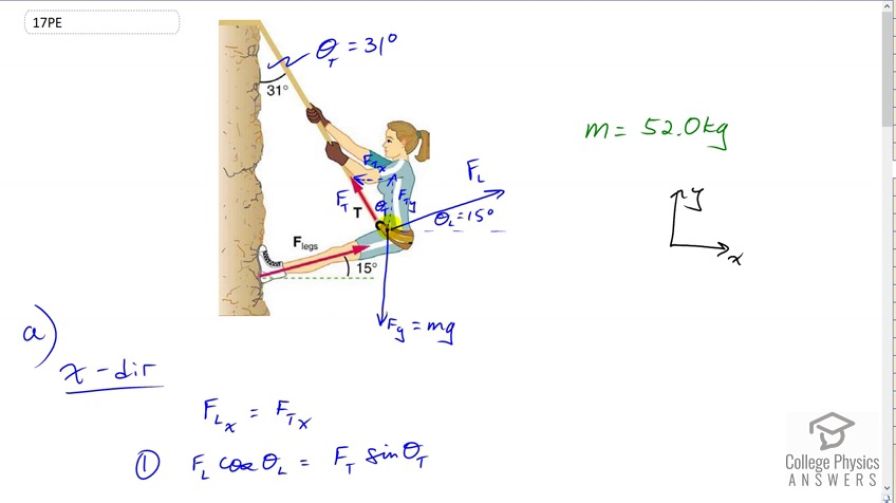
This is College Physics Answers with Shaun Dychko. This climber has three forces on her, and I’ve drawn them with the origin on her center of mass in order to make things a little bit more familiar because we usually draw free body diagrams with the forces all originating at the object’s center mass. So I didn’t want the force arrow to be over here, I want it to be here. So I’ve label it F subscript L for legs and it’s inclined at an angle of 15 degrees with respect to horizontal. We also have the force of tension and it has a component that is straight up and a component that is straight to the side and there’s this angle here theta T between F Ty and F T and F Ty is parallel to the cliff and this angle here and this angle here are interior opposite angles so they are equal. Now I’ve labelled this angle here theta subscript T for tension, it’s 31 degrees. We have force of gravity straight down and there’s no need to turn the force of gravity into components because we defined our coordinate system such that the y-axis is along the line of the gravity, straight up and down. So the other forces do need to be resolved into components. We have force of the legs in the y direction there and force of the legs in the x direction there. If we consider the x direction, we know that the x component of the force due to the legs must be equal to the x component of the force due to the tension of the rope because this climber is not accelerating in any direction so that means all the forces to the right have to equal the total forces to the left and likewise total forces up have to equal the total forces down in order for there to be no acceleration. So force of the legs in the x direction is force of the legs multiplied by cosine of theta L because F Lx is the adjacent leg of this right triangle and so we use cosine to find the adjacent leg multiplied by the hypotenuse. For the x component of the tension force, F Tx is the opposite leg of this triangle and so we use sine of theta T multiplied by F T to find the x component of the force of tension. Well and then there’s not much more we can do with that because there are two unknowns F L and F T, we don’t know either of them and so when there’s two unknowns in an equation, that means you cannot solve it and you must make another equation and so we consider the y direction to find another equation. We know that the force of the tension in the y direction plus the force of the legs in the y direction have to add up to make the force of gravity downwards. F Ty is going to be F T times cosine of theta T and F Ly is going to be F L times sine of theta L and that equals mg, substituting mg in place of Fg there. So now we have two equations and two unknowns, F T and F L are the two unknowns. Let’s do a method of substitution to solve this system of simultaneous equations. We’ll take an equation one version b by dividing both sides by cosine of theta L and we get this equation, F L is F T times sin theta T over cos theta L and then we’ll substitute for that in equation two. So equation two version b, I’ve rewritten it but with a substitution for F L as this instead, I’ve written it in red. So we have F T cos theta T plus F T sin theta T over cos theta L times sin theta L equals mg. The sin theta L over cos theta L can be simplified a little bit into tan theta L. The F T can be factored out because it’s a common factor. So we have F T times cos theta T plus sin theta T tan theta L equals mg. Then we divide both sides by this bracket and we solve for F T. So F T is mg over cos theta T plus sin theta T tan theta L. So that’s 52 kilograms, mass of the climber, times 9.8 newtons per kilogram divided by cos 31, angle of the tangent force, plus sin 31 times tan 15, and we get 512 newtons is the force of tension of the rope. And then to find the force of the legs, we can use equation one b now that we know F T and so the force due to the legs is going to be force of tension times sin theta T over cos theta L, so that’s 512.07 newtons times sin 31 over cos 15, which gives 273 newtons. Now we have to find out what is the minimum coefficient of static friction needed between the girl’s shoes and the cliff. Well we know that the y component of the force due to the legs equals there is a friction, so that is the amount by which this force due to the legs is going up is entirely resulting from friction here and it equals coefficient of static friction multiplied by the normal force. The normal force though is the x component of the force applied by the legs because that’s the force that’s perpendicular to the cliff face. We’ll say that down here again. So F Ly is coefficient of static friction times normal force and the normal force is the x component of the force due to the legs, so we have y component of the force due to the legs equal mu s times x component of the force due to the legs. We divide both sides by F Lx and then switch the sides around, we get coefficient of static friction is the force due to the legs in the y direction divided by the force due to the legs in the x direction, so that’s F L times sin theta L divided by F L times cos theta L, y direction we find with sine and x direction we find with cosine as before, and all the F Ls cancel and this is tangent when you have sine divided by cosine of the same angle. So the minimum coefficient of static friction is the tangent of the angle of the legs which is tan 15 which is 0.27.